Diverse Solutions in Energy System Optimization
By Aditya Sinha with contributions from: Mike Blackhurst, Jeremiah Johnson, Cameron Wade and Paulina Jaramillo
Energy systems models are invaluable planning tools. However, these tools typically produce singular “cost-optimal” solutions that can overlook other solutions that may be more viable when considering non-cost factors. For example, the least-cost strategy may suggest adding nuclear power, which may be constrained by public acceptance. Representing this constraint in a mathematical form in our models can be challenging and thus represents a type of uncertainty. This inherent uncertainty, known as structural uncertainty, underscores the challenge of accurately capturing the complexities of the real-world within a mathematical model. This blog reviews Modelling-to-Generate-Alternatives (MGA), which offers a potential means to address some of the structural uncertainty in our energy system models. MGA slightly modifies conventional least-cost methods, offering a novel and nuanced approach to decision-making in the face of complexity and uncertainty.
A typical optimization-based energy system model has three components:
- Objective function: The objective function describes the overarching goal to be achieved. Energy systems models typically track and minimize the total system cost.
- Constraints: Constraints can encode real-world limits and/or ensure the integrity and validity of the model. For example, constraints in energy systems models govern realistic mass/energy flows and operational constraints of power plants.
- Decision variables: Decision variables represent the levers that the model can manipulate to meet the objective function within the constraints. Examples may include decisions regarding the deployment of technology capacities.
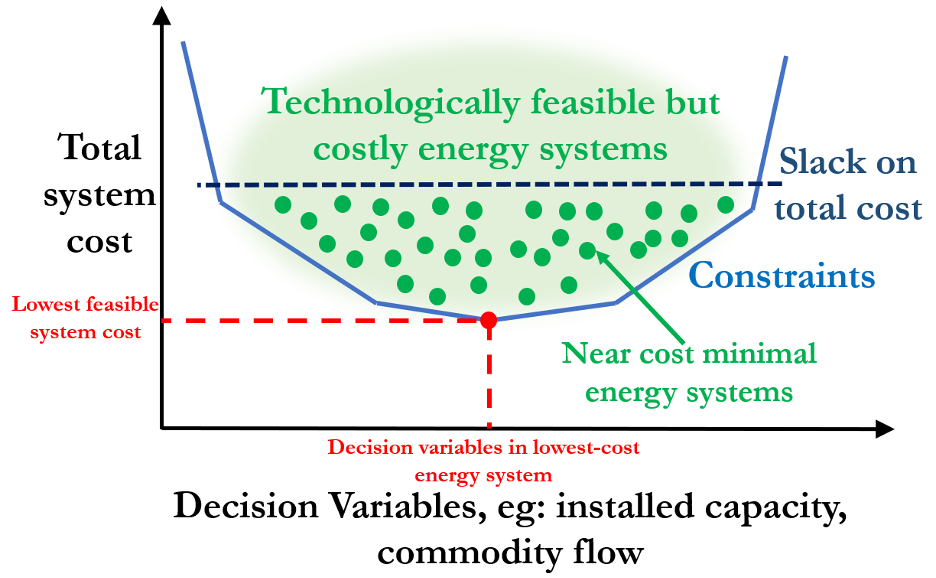
Figure 1: The near-optimal decision space of a linear optimization problem
However, unlike traditional optimization approaches that yield a single solution, MGA provides a portfolio of solutions. MGA is an optimization technique that was initially developed to address land and water management challenges and produce sets of planning alternatives. Consider Figure 1, illustrating the decision space of a typical energy system optimization problem. The solid blue lines delineate the constraints within which a solution must lie. If this problem were to be solved in a conventional linear optimization fashion, the red dot would represent this solution, obtained by minimizing the total system cost, while still respecting the constraints of the problem. By relaxing absolute adherence to minimizing total system cost, MGA can identify additional solutions that are near but not perfectly optimal, as shown by the green dots in Figure 1. The additional solutions MGA can identify are determined by: 1) the “slack” variable, which describes the degree to which solutions can deviate from perfect optimality and 2) the effectiveness with which the new decision space is explored. In the context of energy systems, MGA can identify many energy system designs that have very similar costs, both may be otherwise substantially different. Some of these near-optimal solutions may possess features deemed valuable enough to justify the associated cost premium or fall acceptably within the bounds of other sources of uncertainty (e.g., future conversion efficiencies).
A primary advantage of MGA is in its ability to identify diverse energy system configurations. For example, Figure 2 compares the absolute least-cost solution to two other pathways identified using MGA. The most significant differences between the MGA strategies relate to emissions from electricity, direct air capture (DAC), and carbon capture and sequestration (CCS). One MGA strategy reflects fewer emissions from electricity and more use of DAC. The second MGA strategy reflects more electricity use and CCS. We identified these alternatives as representative groups of many MGA results (using k-means clustering). These pathways differ drastically in system configurations but are otherwise near cost-optimal. Providing a portfolio of options can help decision makers balance many competing criteria (such as equity or public acceptable) at negligible to modest costs increases. However, identifying representative groups using MGA requires thorough exploration of the near-optimal space to avoid biased results.
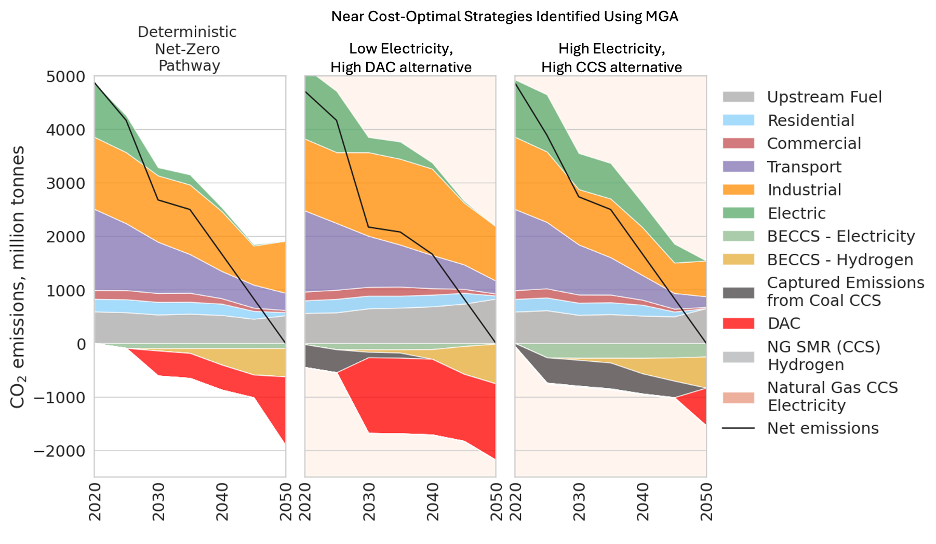
Figure 2: Illustrative pathways from Modeling-to-Generate alternative solutions to examine Net-Zero futures for the United States energy system.
Recognizing that determining the true real-world optimum is practically unattainable due to inevitable uncertainties, MGA offers a pragmatic alternative. Rather than fixating on a single techno-economic optimal solution, which is unlikely to mirror the real-world scenario, MGA advocates for the comprehensive study of the entire near-optimal solution space. Each solution within this space represents a viable real-world alternative, providing decision-makers with a diverse array of options when strategizing for long-term energy systems.